Equal Temperament
On mobile devices, this page is easier to read in landscape
It was Pythagoras who first discovered that notes which blend well together have frequencies of vibration that are related by simple fractions.
For example, the octave is when one note vibrates exactly twice as fast as another.
The perfect fifth (for example C to G) is when the G vibrates exactly 3/2 times as fast as the C.
Here are some building bricks laid out with lengths in the ratio of 3 to 2 - see how the pattern repeats regularly, and how the resulting composite pattern has an innate structure.
![]()
This structure is not so different from the regular pattern of vibration of the eardrum when a perfect fifth is sounded - the eardrum vibrates in a simple pattern, pleasing to the brain.
When two notes do not have this sort of relationship, the pattern does not repeat for a long time, and the vibration of the eardrum changes constantly. Here, the ratio is just slightly more than 3 to 2.
![]()
When a perfect fifth is out of tune, you'll be familiar with the "beating" or vibration that is perhaps once or twice a second, and needs to be slowed to zero to get the fifth "perfect".
The problem
There's a problem. Indeed, the problem has been known to occupy whole books about tuning, but we can cut to the chase in one page.
Suppose we start at bottom C on the piano, and go up in perfect fifths - C G D A E B F# C# G# D# A# F C.
In 12 steps we have got back to C, just as we arrive at the top reaches of the keyboard.
Each time we have gone up, we have increased the frequency by 50%.
After 12 steps we have gone up in frequency by 1.5 to the power 12 which is 129.75. Here's a picture...
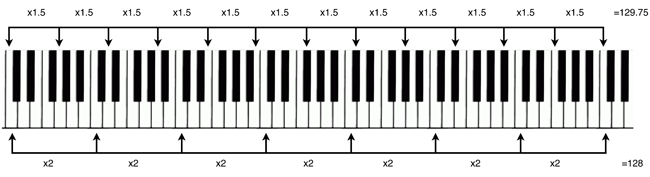
But we've gone up exactly 7 octaves, and each has double the frequency, so we have gone up in frequency by 2 to the power 7, which is 128.
Does not compute!
In order for the octaves of the piano (and indeed the guitar) to be perfect, the fifth needs to be slightly smaller than 1.5
It needs to be 2 to the power (7/12), which is 1.4983 instead of 1.5.
But that's not in tune!
The tiny flattening of the perfect fifth doesn't notice. If I redrew the top picture in the ratio of 1.4983:1 instead of 1.5:1, it would take about a thousand blocks before the growing displacement was obvious.
In musical terms, the beating between, say, C on the second string and G on the top string, is slower than once every two seconds. It's hard to hear.
And so...
And so in guitar terms, tuning a chord to perfection instead of to "near perfection" will make another chord sound worse! When tuning a guitar, it's vital to try different chords so make sure that the tuning errors (which we have to have) are distributed evenly (so they don't notice) and not unevenly (so they accumulate in certain chords).
Here's an example - play the chord of E in first position, and you will find you can flatten the G string and the chord stays sounding nice. However, if you flatten the G string as much as you can with the E chord still sounding pleasant, you will then find a chord of C sounds intolerably "out" !
When I tune using a tuning fork, rather than a chromatic tuner, I double check my tuning by playing the chords of E and C, and also an open chord of D (just Ds and As). I'm checking to make sure they all sound reasonably in tune, rather than some in tune and some most definitely not!
Download this teach-in
Download an e-book of all the teach-ins
Back to the FAQs contents